A Quick Guide to Using O2DESNet

This guide serves to jumpstart using O2DESNet so you can quickly get into modelling and running your simulation.

If you have not completed installing and setting up the project template, please do so before proceeding. This guide also assumes that you are familiar with the discrete-event simulation paradigm; if you are unfamiliar with this paradigm, head over to this quick introduction.

In this guide, we will create a simulator for a simple M/M/1 queue. This is a queue with a single server where both the random arrival and service times are exponentially distributed.

First, we examine the entities involved in this system:
- Statics: none (for simplicity, there is no physical layout represented)
- Dynamics: queue, server
- Events: customer arrival, start of service, end of service

From this analysis, the eventual project should contain the following classes:

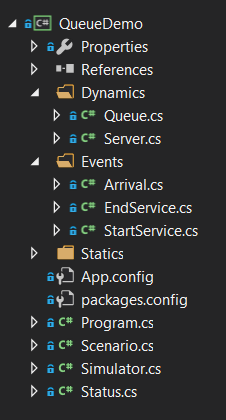
Next, we go through the individual classes.

Statics

Scenario.cs

public class Scenario : O2DESNet.Scenario
{
    public Scenario()
    {
    }
}

As there is no static entities, the Scenario class is empty. Even though it is empty, this class still has to be created and instantiated since it is required by the other classes.

Dynamics

Server.cs

public class Server
{
    public bool IsIdle { get; set; }

    public Server()
    {
        IsIdle = true;
    }
}

Server class represents the server in the queueing system. It has an indicator IsIdle to signify if the server is idle or not. Initially, the server is idle.

Queue.cs

public class Queue
{
    public List<DateTime> TimeStamp { get; set; }
    public int Length { get; set; }

    public Queue()
    {
        TimeStamp = new List<DateTime>();
        Length = 0;
    }
}

The Queue class (not to be confused with Systems.Collections.Queue in C# library) represents the queue in the system. TimeStamp tracks the simulation clock time when a customer joins the queue. Length represents the current length of the queue.

Status

Status.cs

public class Status : O2DESNet.Status<Scenario>
{
    public Dynamics.Queue queue { get; set; }
    public Dynamics.Server server { get; set; }

    public TimeSpan WaitingTime { get; set; }
    public int ServeCount { get; set; }

    public Status(Scenario scenario, int seed = 0) : base(scenario, seed)
    {
        queue = new Dynamics.Queue();
        server = new Dynamics.Server();
        WaitingTime = TimeSpan.Zero;
        ServeCount = 0;
    }

    public TimeSpan GetAverageWaitTime()
    {
       return TimeSpan.FromTicks(WaitingTime.Ticks / ServeCount);
    }
}

The Status class encapsulates all the dynamic entities in the system: Queue and Server. WaitingTime accumulates the waiting time experienced by the customers in the queue. ServeCount tracks the number of customers served. The constructor initializes these properties.

The parameter seed is used as the seed for the random stream DefaultRS.

The method GetAverageWaitTime() returns the average waiting time experienced by the customers that has been served thus far.

Events

In order to obtain samples from the Exponential distribution, MathNet.Numerics.Distributions.Exponential is used. Assume the namespace MathNet.Numerics.Distributions is used.

Arrival.cs

public class Arrival : O2DESNet.Event<Scenario, Status>
{
    public override void Invoke()
    {

        if(Status.server.IsIdle)
        {
            Execute(new StartService());
        }
        else
        {
            Status.queue.Length++;
            Status.queue.TimeStamp.Add(Simulator.ClockTime);
        }

        Schedule(new Arrival(), TimeSpan.FromMinutes(Exponential.Sample(DefaultRS, 1.0)));
    }
}

The Arrival event schedules a next Arrival event based on an exponentially distributed inter-arrival time, which is hardcoded with a rate of 1 per minute. Notice that the random stream DefaultRS is used to generate the inter-arrival time. If a customer enters the queue, the simulation clock time is recorded in Status.

StartService.cs

public class StartService : O2DESNet.Event<Scenario, Status>
{
    public override void Invoke()
    {
        Status.server.IsIdle = false;
        Schedule(new EndService(), TimeSpan.FromMinutes(Exponential.Sample(DefaultRS, 2.0)));
    }
}

The StartService event schedules a EndService event based on an exponentially distributed service time, which is hardcoded with a rate of 2 per minute. Notice that the random stream DefaultRS is used to generate the service time.

EndService.cs

public class EndService : O2DESNet.Event<Scenario, Status>
{
    public override void Invoke()
    {
        Status.ServeCount++;

        if (Status.queue.Length > 0)
        {
            Status.queue.Length--;

            var timeEnter = Status.queue.TimeStamp.First();
            Status.queue.TimeStamp.RemoveAt(0);
            Status.WaitingTime += (Simulator.ClockTime - timeEnter);            

            Execute(new StartService());
        }
        else
        {
            Status.server.IsIdle = true;
        }
    }
}

EndService checks if there is any customer in the queue and services the next customer in queue through a StartService event. It also calculates the waiting time for the customer and updates the total waiting time in Status.

Simulator

Simulator.cs

public class Simulator : O2DESNet.Simulator<Scenario, Status>
{
    public Simulator(Status status) : base(status)
    {
        Execute(new Arrival());
    }
}

The initial event is an Arrival event, which is immediately executed. It is also possible to schedule multiple events initially.

Program (Main)

class Program
{
    static void Main(string[] args)
    {
        var scenario = new Scenario();
        var status = new Status(scenario);
        var simulator = new Simulator(status);
        simulator.Run(TimeSpan.FromHours(48));

        Console.WriteLine("Average Waiting Time is {0}", status.GetAverageWaitTime());

        Console.Write("Press any key to continue...");
        Console.ReadKey();
    }
}

The objects Scenario, Status, and Simulator are initialized in this order according to the constructor parameters required. Refer to the class diagram for more details.

In this example, the simulation is run for 48 hours of simulation time. The average waiting time is printed on the Console at the end of the simulation.

Average Waiting Time is 00:00:30.8494968
Press any key to continue...

The average waiting time is close to the theoretical expected waiting time of 30 seconds, given service rate of 2 per minute and arrival rate of 1 per minute.